√99以上 √1-x^2 積分 492610-1/x^2 積分
X/√(1x^2) の積分 は高校の教科書レベルだ. 答えは, √(1x^2) えーっと,x=sin tとおけば dx=cos t dt だから 分子は x dx= sin t cos t dt 分母は √(1sin^2)=√(cos^2)=cos t で分子の cos と約分して, ∫ sin t dt となるから = cos t = √(cos^2 t) = √(1sin^2 t) = √(1x^2)難:積分√1x^2の積分,√Ax^2の積分,置換と (1)置換積分 (2)部分分數分解 (3)sin,cos,tan,logの基本的なこと (4)$\scriptsize{\displaystyle\int_{}^{}\frac{1}{\sqrt{a^2x^2}}dx=\log\left(x\sqrt{x^2a^2}\right)C}$ (別ページに解説あります。部分積分を使うと、しばしばグラフの形は大きく変わり、例えば、y=1/√(1x 2) のグラフが 描く面積と、y=√(1x 2) のグラフが描く面積の間に、部分積分で導かれるような関係がある ことは、積分を面積の側面から見た時にはきっと新鮮に思われました。

用第二类换元法求下列不定积分1 根号下x 9 Xdx2 Dx 根号下 X 1 雨露学习互助
1/x^2 積分
1/x^2 積分-微積分I 14 53 被積分関数e2x はf(u) = eu,u = 2x と分解すれば合成関数f(g(x)) とみ なせる.u′ = g′(x) = 2 であるので,問題の不定積分を以下のように変形し 置換積分できるようにする. ∫ e2xdx = 1 2 ∫ e2x 2dx 1 2 ∫ eudu 1 2 eu C 1 2 e2x C 上の計算では定理46 を素直に適用した.この適用のしかDec 03, 11 · 広義重積分 f (x, y)=1/√ (1xy) 1417 D= { (x,y)0≦y≦x




求2道积分的1 1 X 根号1 X 2 Dx 2 X 2 4 Xdx 雨露学习互助
数値積分 数値積分を使って,閉形式の解を持たない積分を解く. 記号的には積分できない関数を数値的に積分する: sin (cos x)をx=0から1まで積分 √ ( (1x^2)/ (1x^4) )を積分, x=01 もっと表示19年度微分積分学期末試験問題 理2・3 2124 1月30日(木)5限 (90分) 斎藤毅 ・問題用紙 1枚,解答用紙 a4両面2枚(4ページ),計算用紙1枚. ・筆記用具,計時機能のみの時計 以外も√ 1x2) 山田光太郎 微分積分学第一(4) ( 訂正) 12 / 1 例6 ∫ √
数値積分法(台形則・simpson則・二重指数関数型数値積分法(DE公式)) 概要 ・台形則・simpson則・二重指数関数型数値積分公式(DE公式)による数値積分の 収束の様子を比較します。 使い方 ・左側のボックスから積分する関数を選びます。とする。このとき積分 ∫ D 2 √ 1 x2 y2 dxdy を計算せよ。 解答変換x = rcos , y = rsin はr;ただし,r 0,0θ 2π,0 ϕ π の範囲で考える.このとき積分領域は f ( x,y,z ) 2 R 3 ;
Jul 21, 16 · x^2/√(1x^2)の不定積分を教えてください ベストアンサー:x^2/√(1x^2)={(1x^2)/√(1x^2)}1/{√(1x^2)} =√(1x^2)1/{√(1x^2)} 1/{√(1x^2 1May 25, · この記事では、√1x^2の積分について2通りの方法で解説します。2通りの方法とは、置換積分と部分積分での方法で、好きな方で覚えていただくと良いと思います。最後には、例題も用意していますので、例題を見ながら理解していただくのもおすすめです。11年12月日微分積分II(藤岡敦担当)授業資料 1 x10曲面積 閉区間a;bでC1 級の関数f(x)に対し, 曲線y = f(x)の長さが定積分∫ b a √ 1(f0(x))2dxによりあたえられることは1変数の微分積分でも扱われ



How Come You Halve The Integral Of 2x 1 2 Dx Quora




Ex 7 4 24 Integration Dx X 2 2x 2 Equals A X Tan 1 X 1
Jul 04, · お久しぶりです。だいぶブログを更新せずに放置してしまいました。というのも、数学をやる時間が減ったことに加え、面白い話題が見つからなかったのです。 今回ようやくブログを再開したのは面白い話題が見つかったわけではなく、このブログを勉強した内容をメモしておく場に変更Oct 04, 12 · x^2/(1x^2)√(1x^2) 積分お願いします x^2/(1x^2)√(1x^2) 積分お願いしますOct 12, · 未来や数学と戯れるポメラニアンのブログ √(1x^2)coshax0,1などの定積分 投稿日年10月12日年10月12日投稿者ぽじぽめコメントをどうぞ \begin{alignat}{2} &(1) \displaystyle\int_0^1 \sqrt{1x^2}\cosh axdx=\frac{π}{2a}I_1(a)\\ &(2) \displaystyle\int_0^1 \frac{\cosh ax}{\sqrt{1x^2}}dx=\frac{π}{2}I_0(a)\\ \end{alignat}ただし 全て \(a \gt 0\) <証明> 途中、次の定積分




Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C




用第二类换元法求下列不定积分1 根号下x 9 Xdx2 Dx 根号下 X 1 雨露学习互助
√ 1 x2 z √ 1 x2 となり,z の範囲が複雑になります.うまくD の体積を重 積分で求める方法はありますか. A x, y を固定すると,2番目の式はでてこないのでは?Jun 06, 21 · (tan^{1}x)^2/x^2√(1x^2)0,∞などの定積分;問題3 x= sinθ (π/2 ≦ θ ≦ π/2) とすると dx = cosθdθ 1/√(1x^2)=1/cos 問4と6が問題ですね。これらの積分は大学の教養課程で解いておりましたので思い出しながら解きましたが、問4は中々思い出さず、数時間かかりました。




超越函数e X 2 的定积分 Norstc的博客 Csdn博客



What Is The Integral Of 2x 2 2x X 2 Quora
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history∫ 2x*√1x 2 dx 令 u=1 x 2 du=u'*dx è ∫ √(1 x 2 )2xdx = ∫ √u du = 2/3 u 3/2 C = 2/3 (1x 2 ) 3/2 C 計算積分的微分時,要先看積分的下限是否是常數,若不是就先換,換完後,確認積分的上限是否和 dt 一樣,不一樣就假設 u= 上限再算積分の視覚的表現 このページをダウンロード Wolfram言語を使っています WolframAlphaのご利用についてのご質問は Proプレミアムのエキスパートサポートまで お問い合せください »




1除以根号下2x X方积分



不定积分x E 1 Dx 计算不定积分 E的1 X次方 X平方dx
X 2 y 2 z 2 a 2 g で,これは極座標変換で積分表 定義 不定積分 定積分 黎曼積分 達布積分 勒貝格積分 積分的線性 (英語:Linearity of integration) 求積分的技巧( 換元積分法 · 三角換元法 · 分部積分法 · 部分分式積分法 · 降次積分法 ) 微元法 · 積分第一中值定理 · 積分第二中值定理 · 牛頓解説と解答例 0 関数f(x) の不定積分は,f(x) の原始関数(x に関して微分するとf(x) になるような関数) F(x) に不定定数を足したF(x)C という形になるのでした.このようなF(x) が簡単に見つ かる場合には,それを使えばいいわけです. (a) (ex)0 = ex だからZ ex dx = ex C (b) Z




1 X 2 1 積分5 Lnzikz



Dx X 根号下 1 X平方 的不定积分 作业 慧海网
Aug 15, 19 · 自分の計算だと、違う答えになります。 y=arcsin (√ (1x^2))とすると、 √ (1x^2)=siny dy/dx=1/ (dx/dy)√ 1x2 ∫ 1 p 1x2 dx} 632 置換積分 p 1x2 = t x と置けばx2 1 = (t x)2 従ってx = t2 1 2t です。また √ 1x2 = t x = t2 1 2t;) 2 R2 0 r 1;




How To Integrate 1 X 2 1 2 Quora




Integral Of X 2 Sqrt 1 X 2 Substitution Youtube
Jan 07, 13 · 看板 Math 標題 Re 微積 函數根號做積分 時間 Mon Jan 7 13 ※ 引述《pigheadthree (爬山)》之銘言: 題目類型:函數根號做積分 f (x)= 1x^ (2)^ (1/2) 積分f (x) 小弟實在無從下手,也無想法可解! 實在是想不出來該如何解法! 麻煩版上前輩們不吝嗇についてC1 級であり、この変換によって領域 D′ = {(r;Sep 22, · f(x)=x/√(1 x^2)でも置換積分を使うけど、三角関数は使わない。 t^2=1x^2とすると、積分範囲は0~1/2から1~3/4に変わる。 2t(dt/dx)=2x t dt= x dx ∫0, 1/2 x/√(1 x^2) dx =∫0, 1/2 (1/√(1 x^2)) x dx 0≦x≦1/2の範囲では √(1 x^2)>0 より、 =∫1, 3/4 (1/t) t dt =∫1, 3/4 1 dt
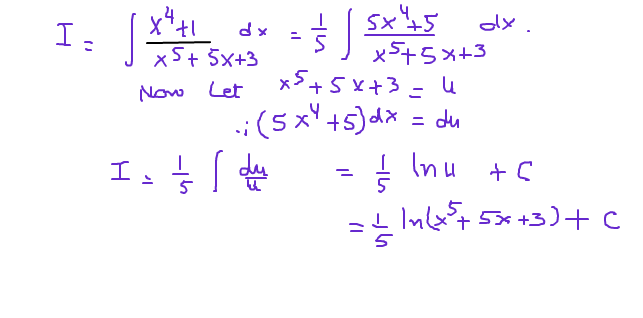



How Do You Integrate Int X 4 1 X 5 5x 3 Socratic
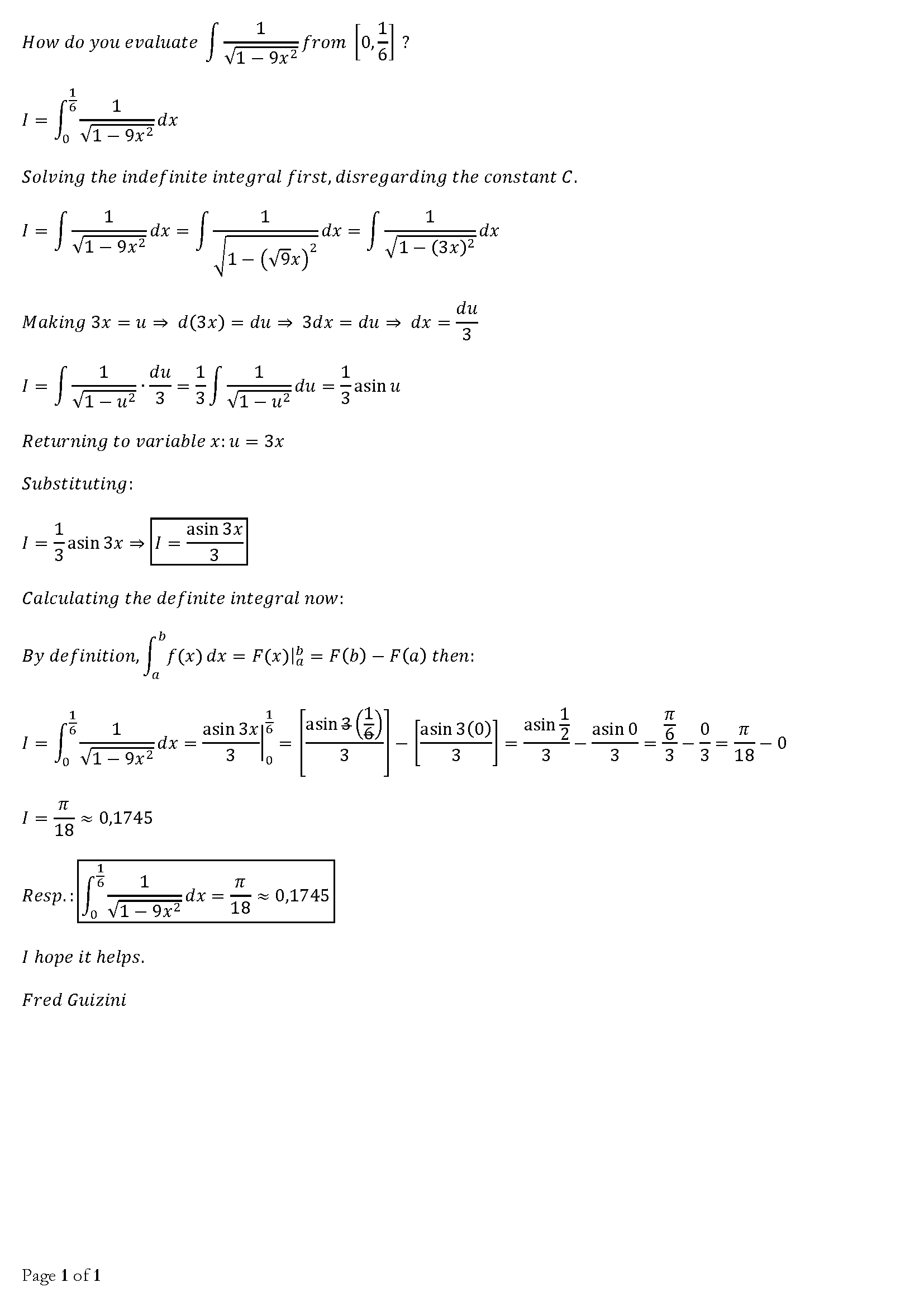



How Do You Evaluate Int1 Sqrt 1 9x 2 Dx From 0 1 6 Socratic
を上積分,下積分とよんで,それらが一致するときに可積分といい,その値 を重積分という. このときには,あとで述べる広義積分の場合と異なり,関数を正負に分け る必要はない. 例4 (錐の体積) 簡単のため,底辺の長さが2,高さが1 である四角錐を考√ 1x2 1 2 log x √ 1x2 C が得られます(ただし、C は積分定数です)。 以上まとめると次の通りです: 事実631 ∫ 1 p 1 x2 dx = Sin 1xC (61) ∫ √ 1 x2dx = 1 2 {x √ 1 x2 Sin 1x} C (62) ∫ 1 p 1x2 dx = log (x √ 1x2) C (63) ∫ √ 1x2dx = 1 2 {x √ここでは、 不定積分 I= √ 1 1 x 2 d x を求めてみる。 高校数学で登場する積分の中ではかなり面倒な方の部類に入るだろう。 久々に積分の計算をしたせいか、 多少苦労してしまったので、 まとめておく。 高校範囲での計算 まず、 x > 0 とする。




積分 1 Sqrt E X 1 Youtube




1 根号下 1 X平方 立方乘以dx 求定积分 雨露学习互助
注意到∫sectdtant=∫ (sect)^3dt 故原积分= (1/2)sect*tant (1/2)ln (secttant)C 最后再作变量还原即得结果: (1/2)x* √ (1x^2) (1/2)ln (x√ (1x^2))C 赞 评论 微信分享 微博分享 打开微信"扫一扫"分享给朋友 举报0 2ˇ} 標準H41W1712 名古屋大学・理学Dx dt = 2t 2t (t2 1)2 4t2 = t2 1 2t2 なので、 ∫ √ 1x2dx = ∫ t2 1 2t t2 1 2t2 dt = ∫ (1 4 t 1 2t 1 4t3) dt となって ∫ √ 1x2dx = 1 8 t2 1 2 logjtj 1 8t2 C = 1 2 t2 1 2t t2 1 2t 1 2 logjtjC = 1 2 x √ 1x 2 1 2 log x √ 1x C C は積分定数です)。 事実631 ∫ 1 p 1 x2




Int 2 2 X 3cos X 2 1 2 Sqrt 4 X 2 Dx




怎麼求1 X X 3 的積分 人人焦點
Oct 12, 08 · ∫x^2√(1-x^2)の不定積分の問題なんですが, つぎのように解いてみたんですが, ∫x^2√(1-x^2)dx =3x^3√(1-x^2)∫x^3√(1-x^2)'dx =3x^3√(1√1x^2,積分,微分,グラフ,積分,定積分,不定積分,展開,近似,テイラー展開,n次導関数 √1x^2 の商品検索結果 女性のためのヘアケア、女性用育毛剤・育毛シャンプーに関する話題や情報Sep 21, 19 · 今回は無理関数の積分パターンを学習するよ。$\sin$ に置きかえる1$\displaystyle\int_0^1 \sqrt{1x^2}\space dx$こういう形がきたら、$\sin$ に置きかえる。$x=\sin t$




E的x次方定积分x乘以e的负x次方 定积分




How To Solve The Integral Of X 3 1 X 2 3 Quora
積分 x^2*√ (x^21) このように,左辺と同じ積分 ∫ x2√x21dx ∫ x 2 x 2 1 d x が右辺にも現れた.さ」を積分の形で定義した.とくに,定理114(100 ページ)では「グラフの長さ」 の計算式を与えている*5.単位円の定義式 √ x 2y = 1(原点との距離は1)より, x ≧ 0 を満たす半円H はy の関数x = f(y) = √ 1 y2 のグラフとして表現できる.May 24, 19 · 设x=asint,则dx=dasint=acostdt,可以得到: a^2x^2 =a^2a^2sint^2 =a^2cost^2 ∫√(a^2x^2)dx =∫acost*acostdt =a^2∫cost^2dt =a^2∫(cos2t1)/2dt =a^2/4∫ (cos2t1)d2t
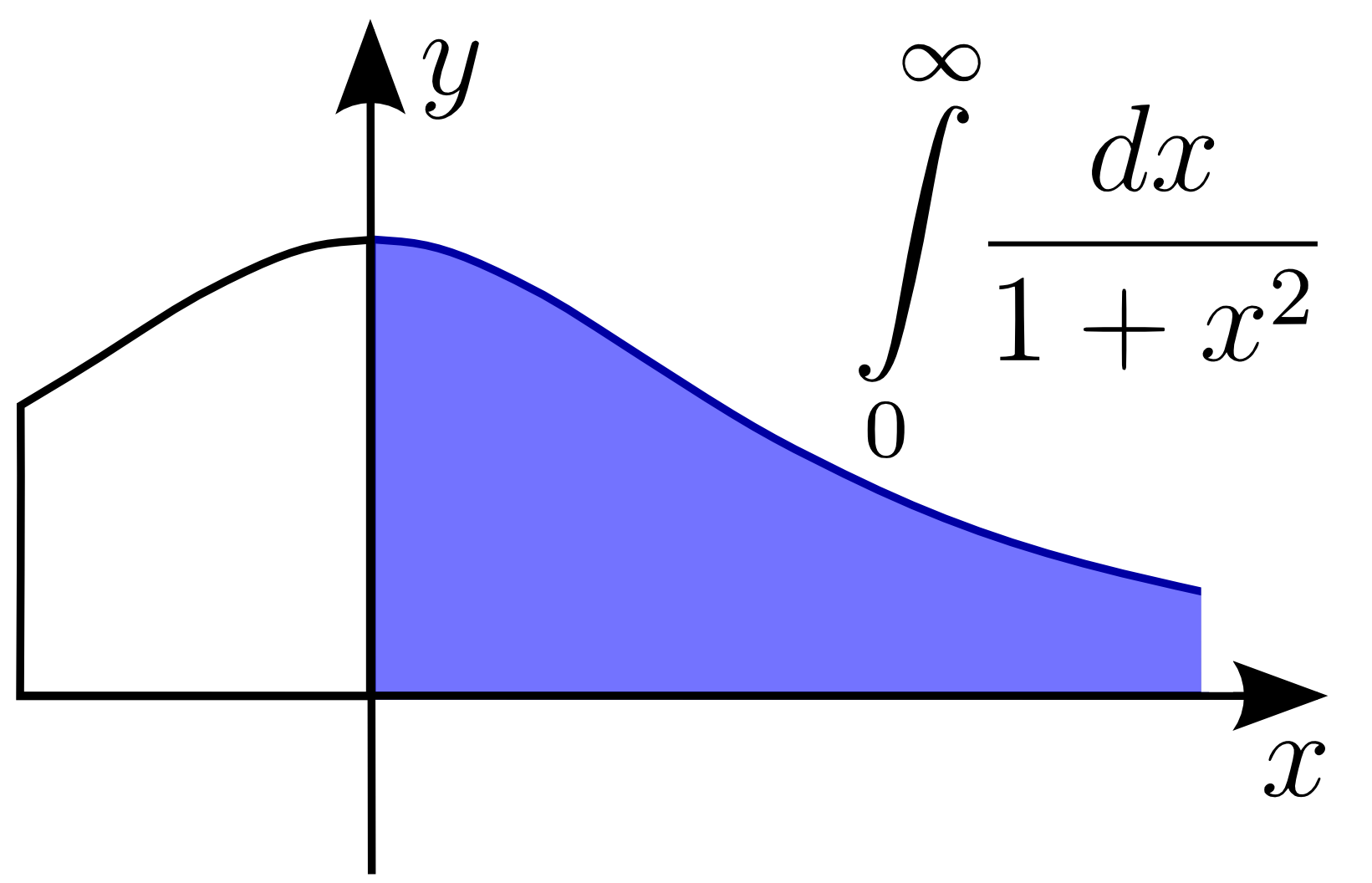



Improper Integral Wikipedia



Integral Calculator With Steps
May 18, · この記事では、特定の 1/√1x^2の積分 について 置換積分を2回 行う方法で解説します。 また、 置換積分を1回でのみ解ける簡略的な方法 についても解説しています。 最後には、例題もありますので、例題を見ながら理解していただくのもおすすめです。 目次 1. ∫ 1 √1 x2dx ∫ 1 √ 1 x 2 d x の積分 2. ∫ 1 √a2 x2dx ∫ 1 √ a 2 x 2 d xH1(y;z) x h2(y;z)g 此處R為y;z平面上的一個平面區域‧於是積分就可以改寫為 ∫∫ D f(x;y;z) = ∫∫ R (∫ h2(y;z) h1(y;z)練習33 (教科書p91 問38)次の関数の不定積分を求めよ。 (1) x √ 1x2 (2) logx x (3) xex2 (4) 1 √ x(1−x) ヒント:(4) はt = √ x とおいてみる。 練習34 (教科書p91 問39)次の定積分を求めよ。 (1) ∫ 1 0 x 1x 2 dx (2) ∫ ˇ=2 0 cosxdx 1sin x (3) ∫ 1 −1 dx ex e−x 定理310




积分公式和常用方法总结 Leemboy的博客 Csdn博客 积分公式




对于似1 1 X 4 型的不定积分的总结 Erasernut 博客园
Sep 21, 19 · 数III無理関数 √1x^2 型の積分 sin に置きかえ 1104 数III複素数平面z で表された式の絶対値の最大と最小を求める国公立基本山田光太郎 微分積分学第一(14) 6 / 28我們當然並不一定要先對z積分‧我們也可以先對x積分,或先對y積分‧這些方式都與前面 類似‧例如,我們想先對x積分,我們就將區域D寫為 D = f(x;y;z) (y;z) 2 R;




求2道积分的1 1 X 根号1 X 2 Dx 2 X 2 4 Xdx 雨露学习互助



Evaluate The Integral Of 1 X2 Stumbling Robot
置換積分・部分積分 問題1 解答 1 置換積分法を使って次の不定積分を求めよ ただし, 積分定数はC とせよ (1) I = ∫ xex2 dx 解 t = x2 とおく dt = 2xdx より置換積分法を使うと I = ∫ et 2 dt = et 2 C = ex2 2 C (2) I = ∫ sinxcos4 xdx 解 t = cosx とおく dt = −sinxdx より4/15 arcsin, arctanの関係と,導関数. 逆関数の微分. 例題 √(1x^2)の不定積分を求めよ. 平均値の定理 と 最大値の定理,中間値の定理. 全称命題,存在命題とその順序、論理記号、写像の定義. 4/22 微分方程式.ことばの定義,初期値問題.




Calculus Integration Techniques Trigonometric Substitution Wikibooks Open Books For An Open World




Integral Xsinx 1 Cos 2 X Dx I Get That In Walfram Www Wolframalpha Com Input I Integral Xsinx 2f 281 2bcos 2x 29 But It Does Not Help Enotes Com



数 次の不定積分を求めよ 1 Dx X X 2 2 Yahoo 知恵袋




How Do You Find The Antiderivative Of Int 1 X 2 10x 29 Dx Socratic
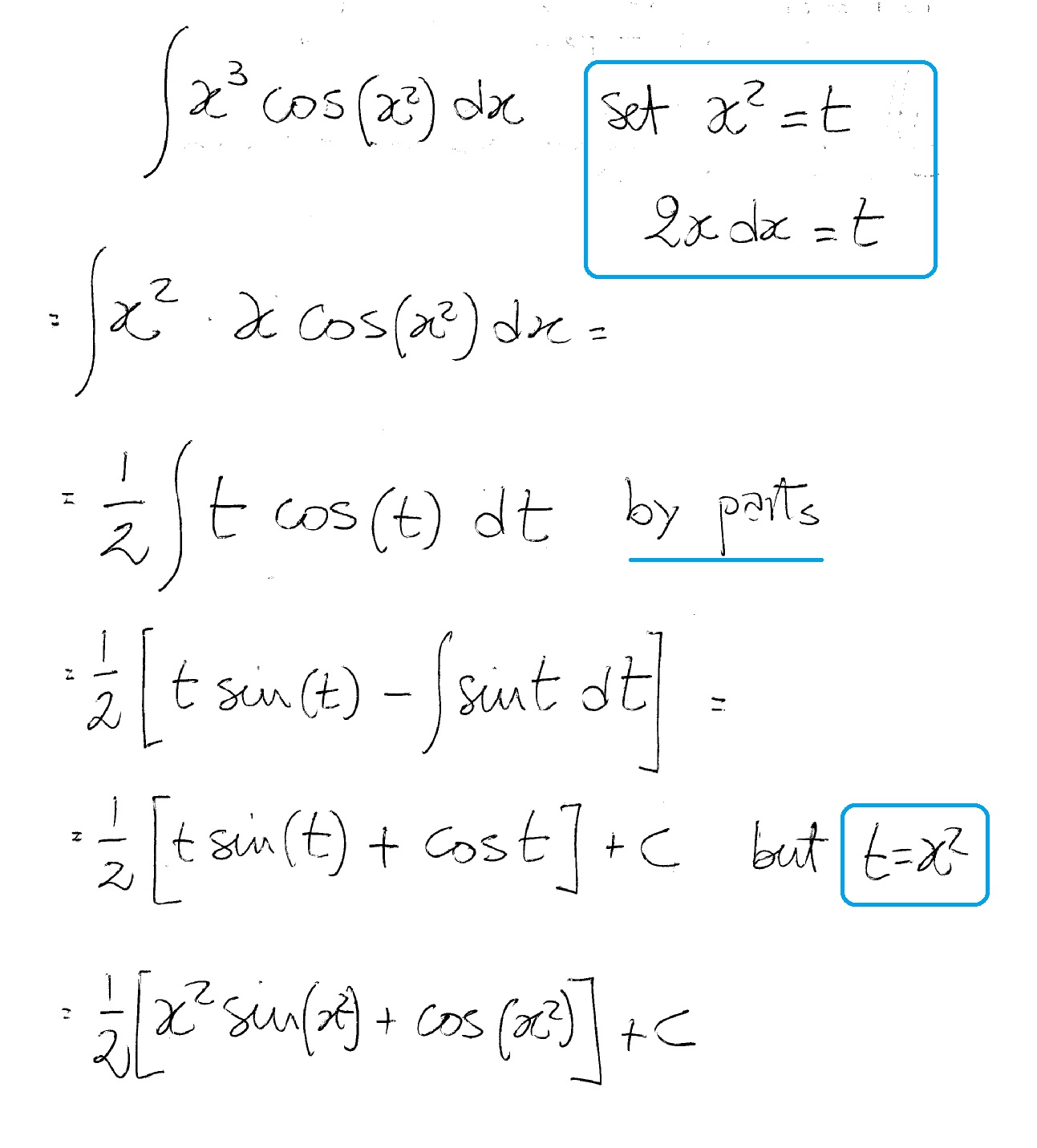



How Do You Integrate X 3cos X 2 Dx Socratic
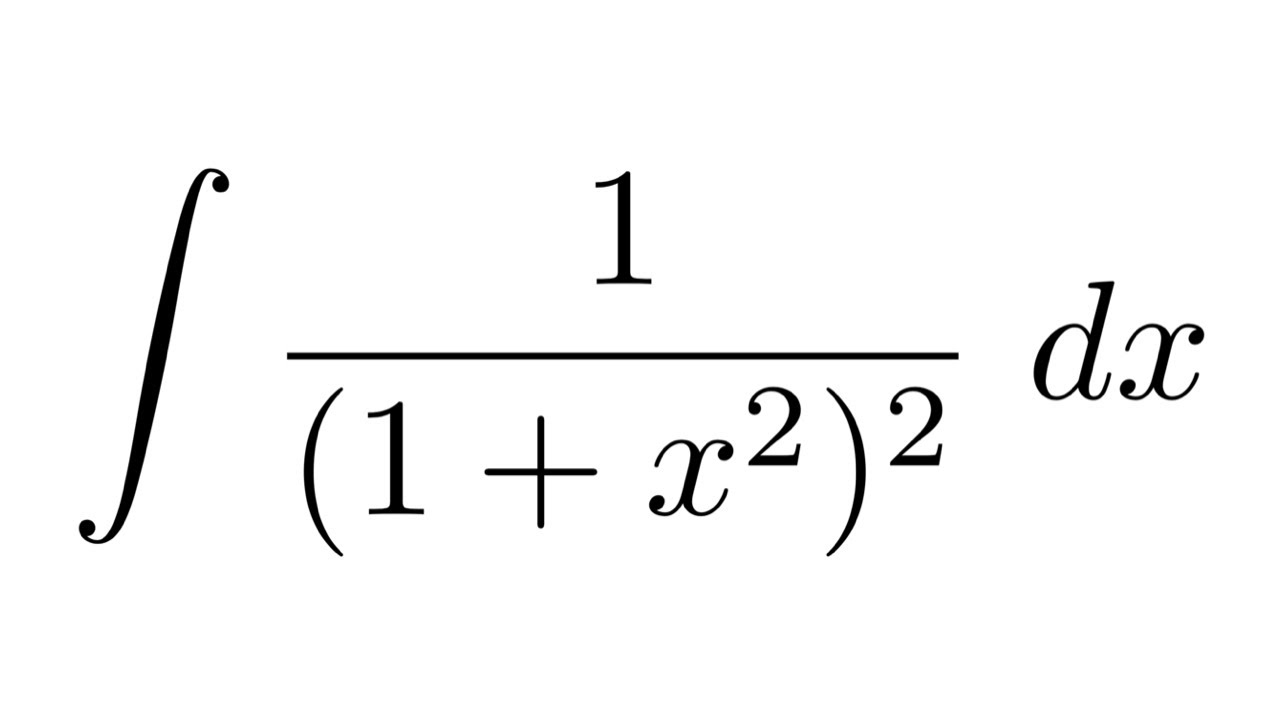



Integral Of 1 1 X 2 2 Substitution Youtube



二重积分的计算二重积分的计算 领域开拓网




Evaluating Int Sqrt 1 T 2 Dt Mathematics Stack Exchange
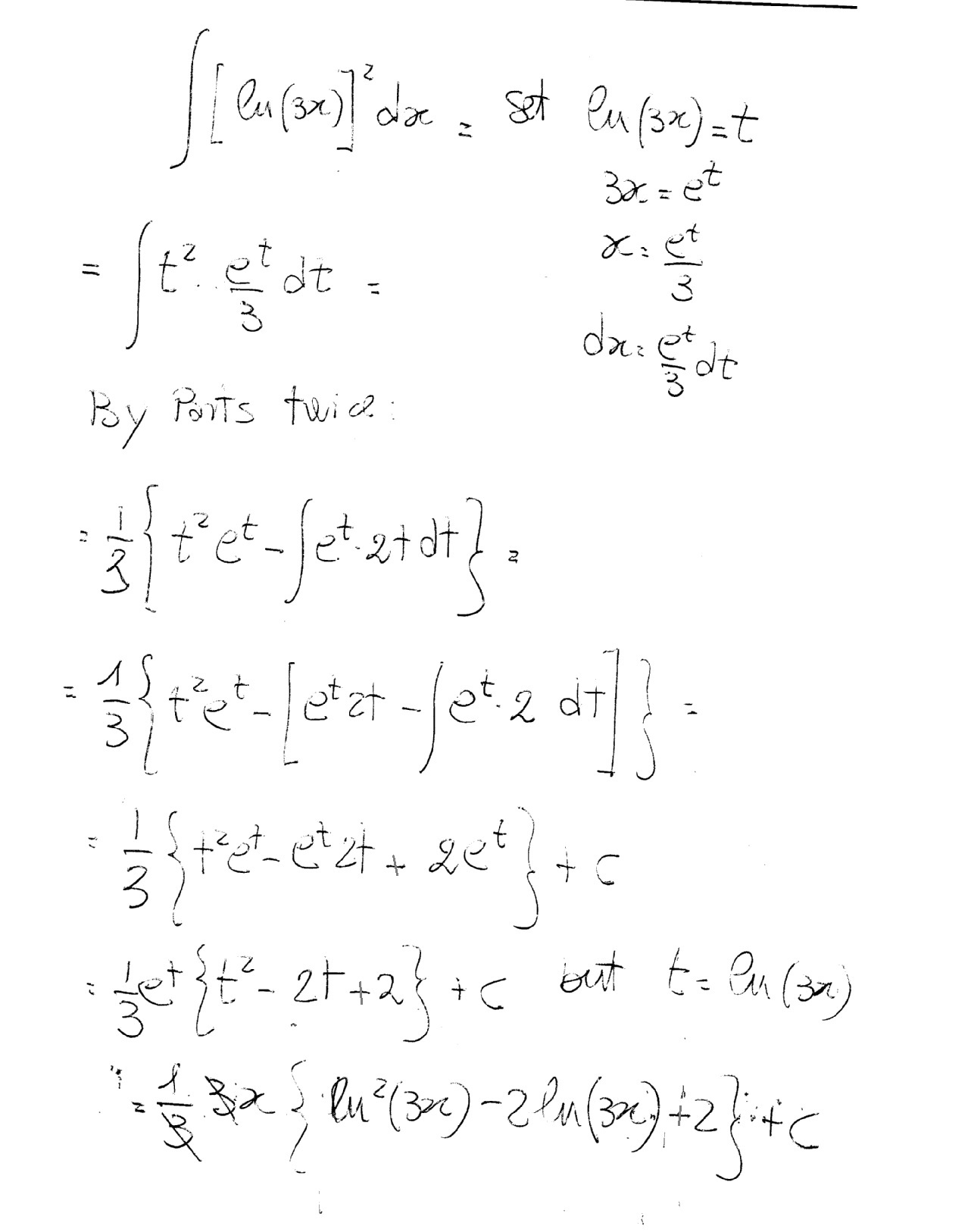



How Do You Find The Integral Ln 3x 2dx Socratic




对于似1 1 X 4 型的不定积分的总结 Erasernut 博客园
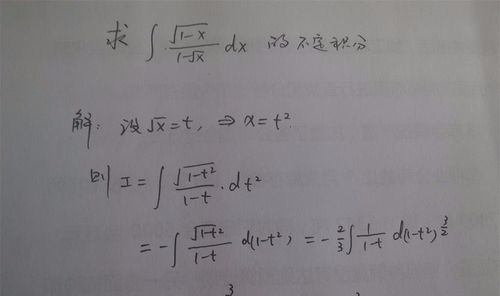



求 1 X与1 X的商的不定积分 搜狗指南




大學高等數學 第三章第二講不定積分換元積分法 壹讀




Evaluating Int Sqrt 1 T 2 Dt Mathematics Stack Exchange



Evaluate The Integral Of 1 A Bx2 Stumbling Robot
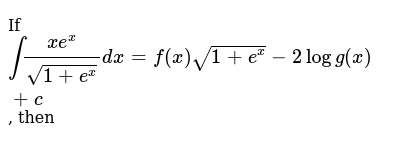



If Int Xe X Sqrt 1 E X Dx F X Sqrt 1 E X 2logg X C Then




Calculus Integration Techniques Trigonometric Substitution Wikibooks Open Books For An Open World




1 X 29 X 2 Dx2 X 2 1 急 不确定积分 多次操作 详细过程 好加点o 365bet送彩金 365注单审核不能提款




X 3 X 2 1 の不定積分 申し訳ありませんが 画像を作成しましたの 数学 教えて Goo




Calculus Integration Techniques Trigonometric Substitution Wikibooks Open Books For An Open World




How Do You Integrate 1 X 2 Sqrt 1 X 2 Socratic



急求数学帝解答exp X 1 Exp 2x 积分过程我知道答案是atan 1 Exp X 1 Exp X 但是自己积分怎么就积分 不出来呢 我是令t Exp X 然后化成1 T 2 1 1 T 2 积分 但是这样的结果是 Exp 1 Arctan Exp X 作业 慧海网




求不定积分xe X 1 X 2 Dx 雨露学习互助
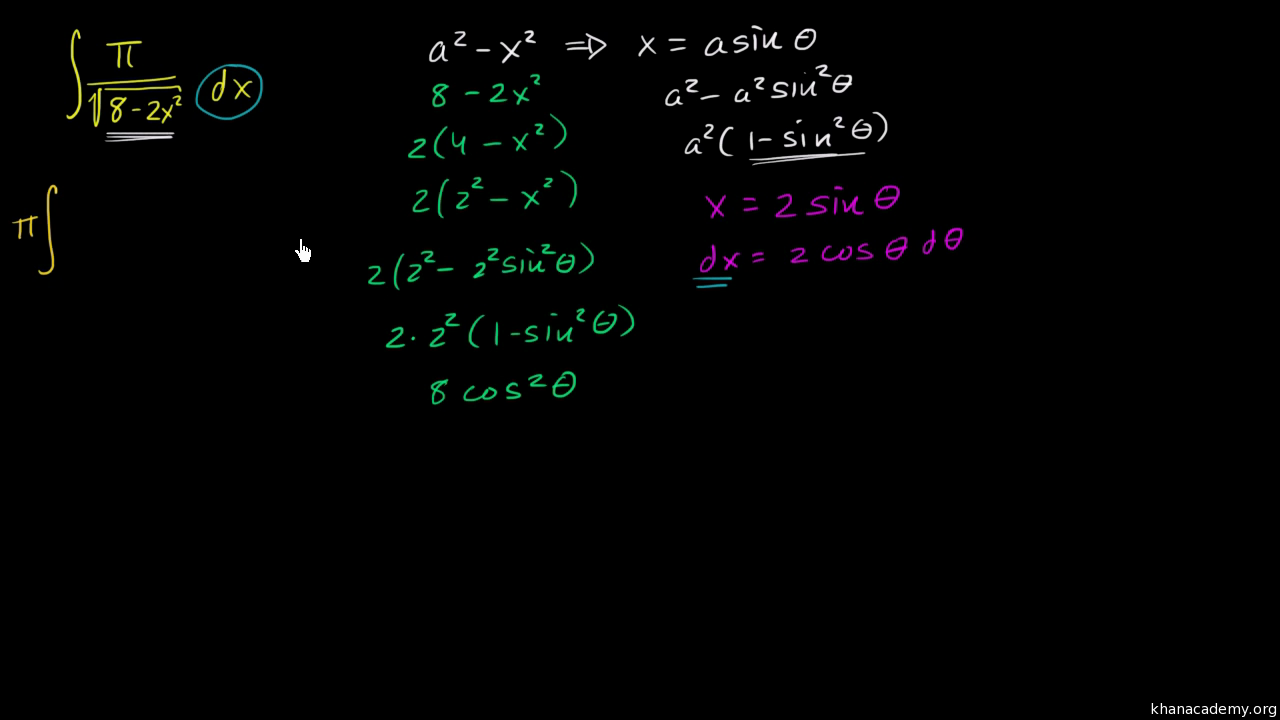



Substitution With X Sin Theta Video Khan Academy




實用特殊積分求法 每日頭條



高数求定积分0到1 Ln 1 1 X 2 Dx咋做呀 作业 慧海网




Integral Of Sqrt 1 X 2 Substitution By Parts Youtube




求不定积分 Ln 1 根号x Dx 雨露学习互助
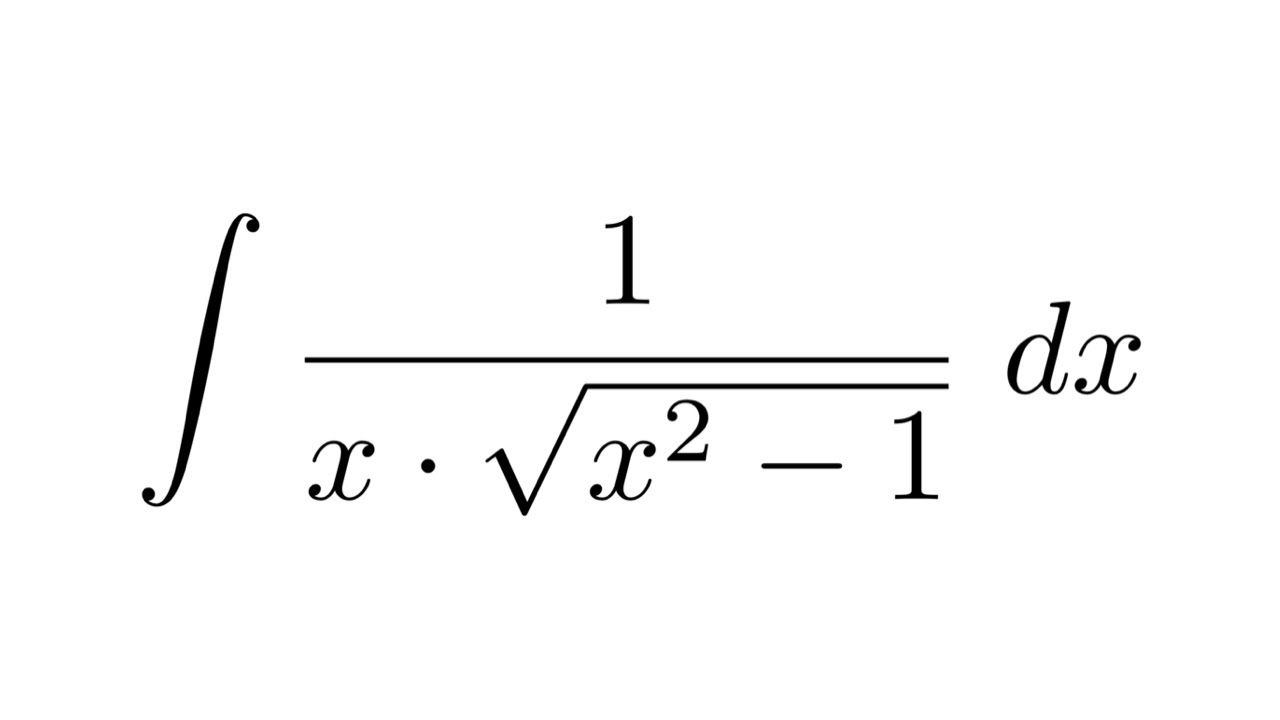



Method 1 Integral Of 1 X Sqrt X 2 1 Substitution Youtube




置換積分の方法 置換方法を覚えておきべき積分問題 大学入試数学の考え方と解法



二重积分计算计算二重积分 领域开拓网




What Is The Integration Of 1 Xe X Quora




无法求不定积分怎么求定积分 怎么求arcsinx的不定积分 三人行教育网 Www 3rxing Org




Int Dx X 1 3 4 X 2 5 4 Equal To A 4 X 1 X 2



1 X 1 Dx积分从1到3 作业 慧海网



知識家 單元16 5 代換積分 X 1 X Dx A 這是個數學愛好者的樂園 歡迎大家都能夠來分享 思考數學題目 隨意窩xuite日誌
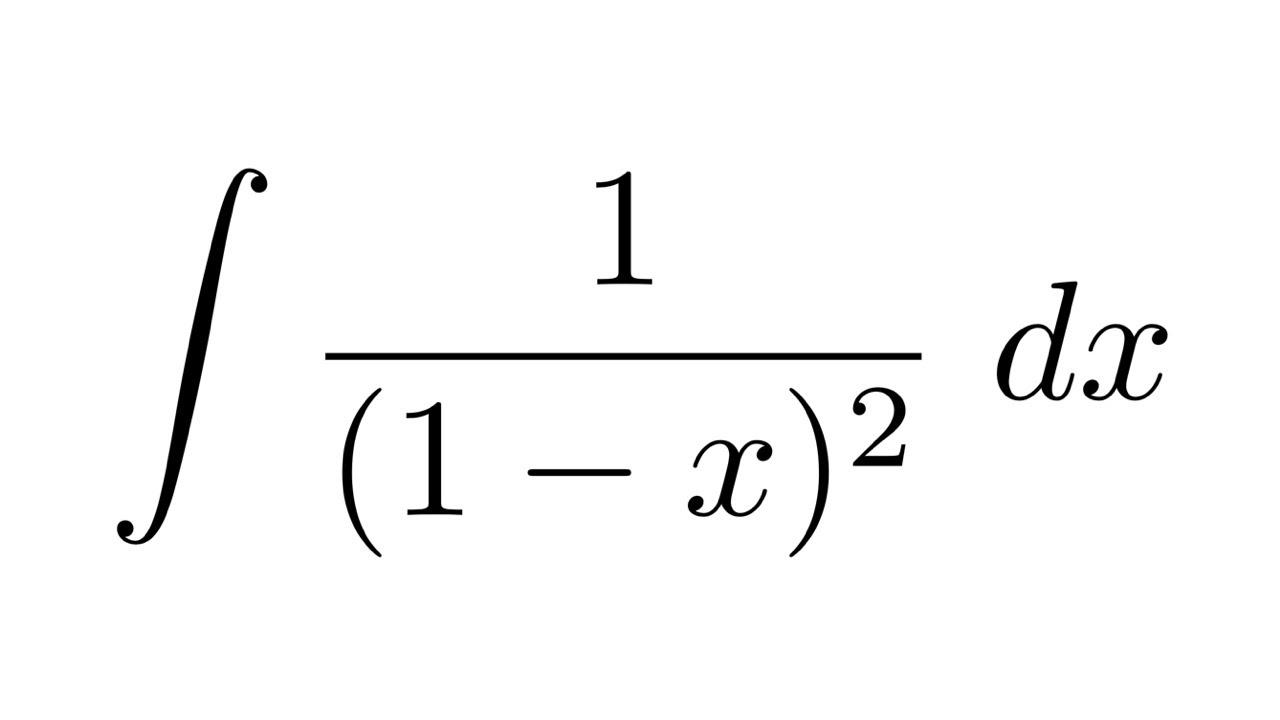



Integral Of 1 1 X 2 Youtube



How To Integrate X Sqrt X 2 Y 2 With An Order Dxdy Quora




Gaussian Integral Wikipedia




What Is The Integral Of Dx 1 3x 2 Quora



Cos X 2 Dx 万图壁纸网




Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C




Gaussian Integral Wikipedia
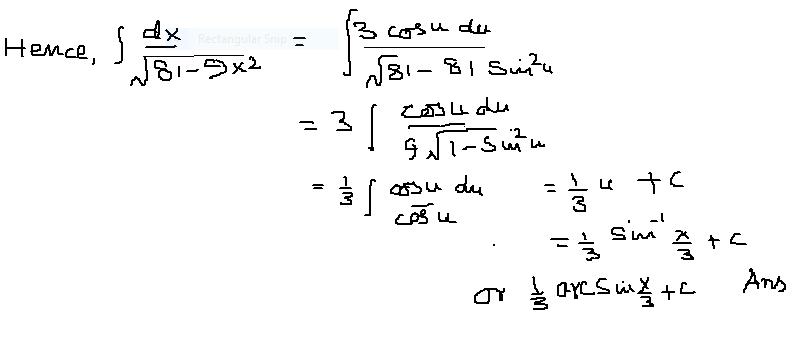



How Do You Integrate Int Dx Sqrt 81 9x 2 Using Trig Substitutions Socratic




What Is The Integration Of 1 Sinx 1 2 Quora



求不定积分 1 X Dx 根号下 1减x的平方 数学解答 作业小助手




Contour Integration Wikipedia



How To Integrate 1 X 2 3 2 Quora
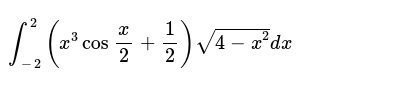



Int 2 2 X 3cos X 2 1 2 Sqrt 4 X 2 Dx



What Is The Integral Of Dx Sqrt X X 2 Quora




How To Integrate Math Int Sqrt X 3 1 Dx Quora




6 2 4 1 部分分式積分法int 1 2x 1 X 1 Dx Youtube



求不定积分 根号下x平方减a平方 Dx 急 学生作业帮 兵器谱



Evaluate The Integral X 1 3x 2 4x 3 Dx Sarthaks Econnect Largest Online Education Community




Fresnel Integral Wikipedia




对于似1 1 X 4 型的不定积分的总结 Erasernut 博客园




Integral Of 1 Sqrt 1 X 2 Substitution Youtube




求不定积分 Xarctanx 1 X 2 Dx 雨露学习互助




不定积分x 3 Sqr 1 X 2 3 Dx 雨露学习互助



定积分证明 Dx 1 X 2 X 0 在 X 1 和在 1 1 X 的定积分相等 作业 慧海网



X2 1 X4 1求不定积分 不定积分 X4 1 X2 1 Dx
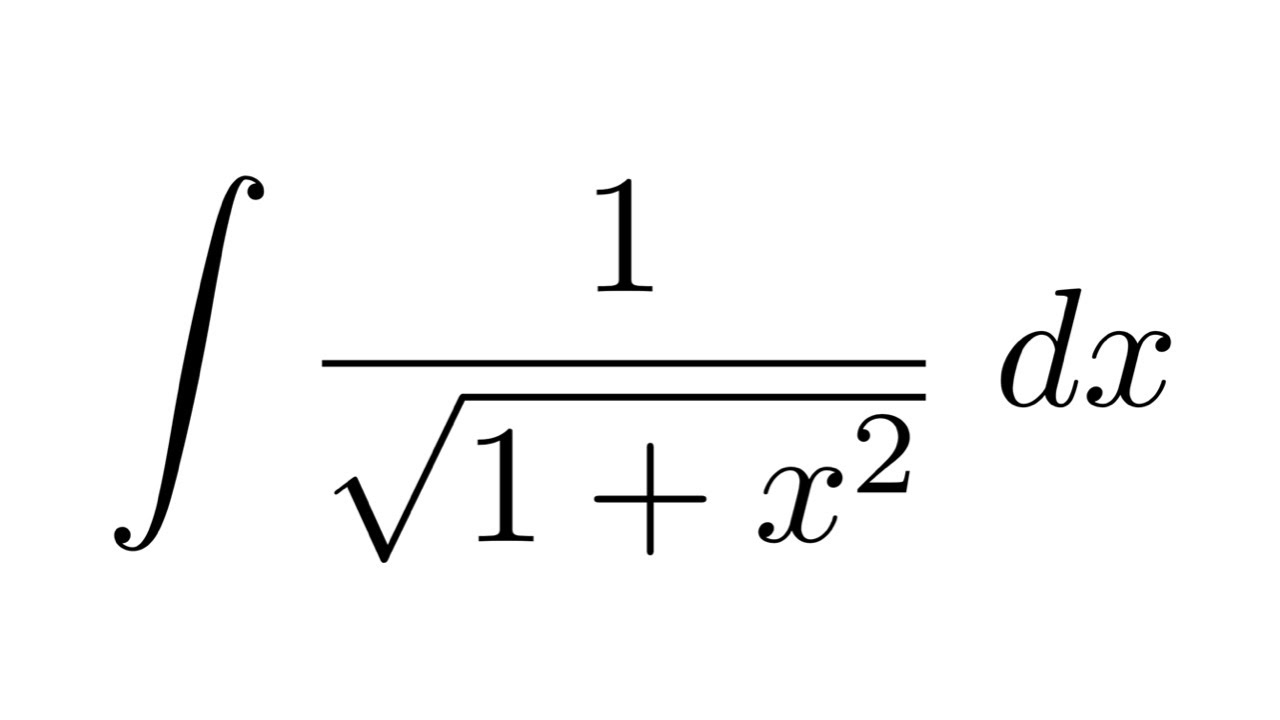



Integral Of 1 Sqrt 1 X 2 Substitution Substitution Youtube



Integral Of Sqrt X 3 1 Dx Physics Forums
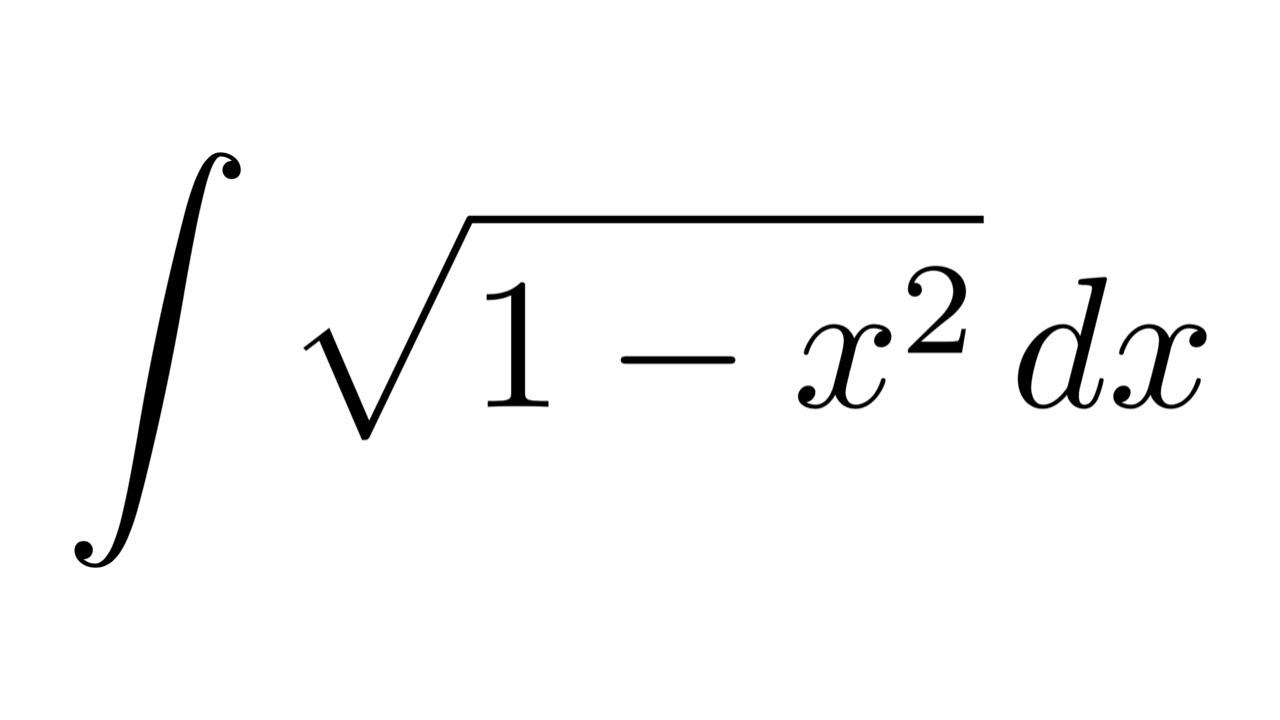



Integral Of Sqrt 1 X 2 Substitution Trigonometric Identities Youtube




求不定积分 X 2 9 1 2 Dx X 雨露学习互助




Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C




Ex 7 4 2 Integrate 1 Root 1 4x2 Class 12 Ncert Ex 7 4




Gaussian Integral Wikipedia




求定积分 上限根号3 下限0 X乘根号下1 X 2 Dx 雨露学习互助




高数不定积分求解 Ln 4 X 2 Dx 雨露学习互助



How To Integrate 4 X 2 1 2 Quora




求不定积分 1 二次根号下 E的x次方加二 雨露学习互助




8 Ways To Integrate Wikihow




How Do You Find The Antiderivative Of Int Sqrt 9 4x 2 Dx Socratic
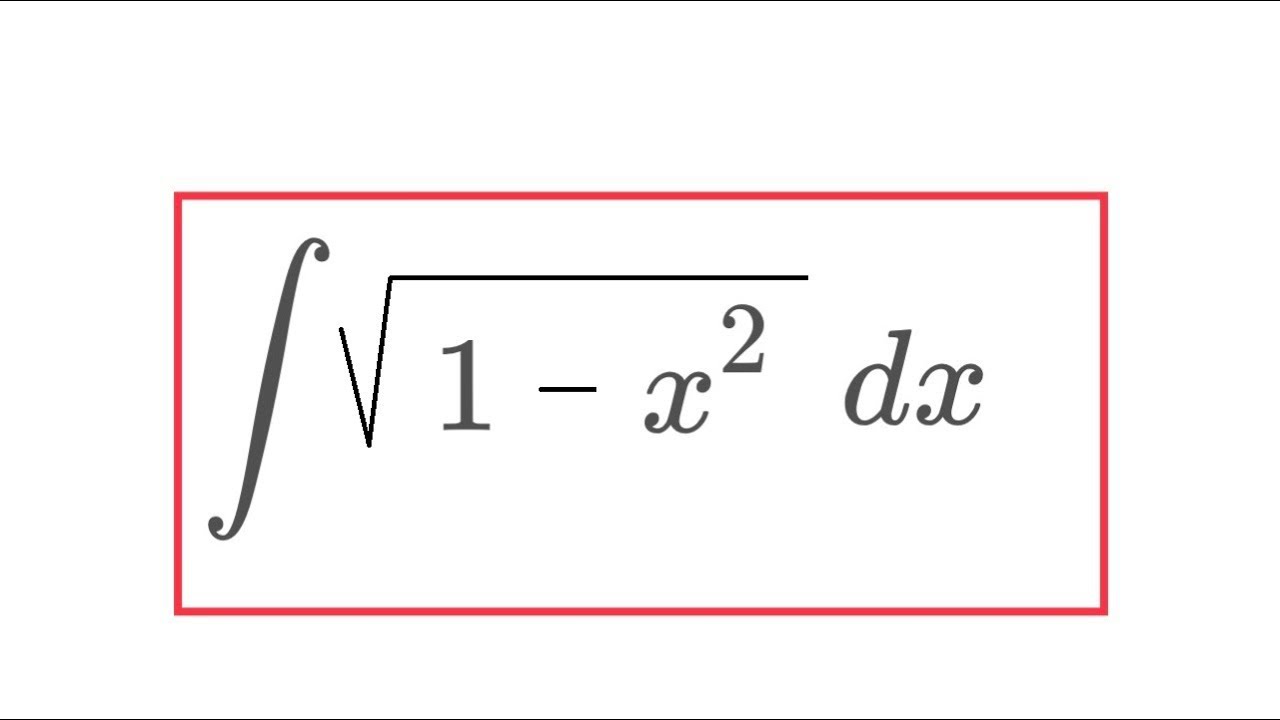



Integral Sqrt 1 X 2 Youtube


コメント
コメントを投稿